tl;dr: there are many studies looking at the IFR of covid-19, their statistical analyses are of varying quality.

It’s a story almost as old as time – scientist meets fashionable hypothesis, falls in love, extracts statistics from data and publishes, at which point the hypothesis is elevated to the status of backed-by-science™. Once enough studies have been written, these are aggregated by meta-analyses, and eventually there is scientific-consensus™. If the hypothesis is true (and it often is), the story ends here and everyone lives happily ever after.

A second story says “Why Most Published Research Findings Are False”, that studies tell us very little about causation, the replication crises, p-hacking and much more.

I do not think I am being controversial in saying that “hard” sciences with clearly testable predictions like physics and chemistry tend to follow the first story, whereas “soft” sciences like economics, psychology, epidemiology, medicine or sociology sometimes have a tendency to publish results that are wrong, even repeatedly. Optimists say that unlike money, good reasoning drives out the bad, and the sustained focus on replication crises when they happen supports this view. But what if there is no time for this process to take place?

A global pandemic with an immediate need for good science

In principle, we know that many fields are plagued by poor practices. In practice, I hear no mention of the elephant in the room – covid-19 epidemiology research. Everybody cares about the infection fatality rate/risk (IFR), so it is important to assess the quality of the best studies that tell us what this number is.

As with everything in life , there is a lot uncertainty. Luckily, statisticians have developed tools for systematically dealing with uncertainty. But statistics is hard, with statisticians saying “we have to accept statistical incompetence not as an aberration but as the norm”. I’m sure I’m not the only one asking themselves whether statistical incompetence is also the norm in covid-19 research. I decided to look at some studies from the field.

Disclaimer: I’m wary of the effects of writing/sharing a blog post like this – after all, those people who claim that coronavirus “is just the flu” or ” doesn’t exist” or “is caused by Bill Gates” will surely use posts like this as evidence claiming their views are scientific. To those people: Just because the scientists make mistakes does not mean you are right. If anything, becoming more confident in your view after reading a post that says the science is less clear makes no sense! Uncertainty cuts both ways, not just towards your preferred hypothesis.

Too many studies, too little time to review them all

I had to somehow decide what studies to look at. A meta analysis regarding the infection fatality rate (IFR) was linked fairly prominently on a forum I follow. Despite being published on the 29th of September (these things typically exist as preprints for a while before being published), it already had 40 citations on google scholar when I wrote this. It seemed like the perfect source of studies to review as I didn’t want to wade into the murky depths of studies nobody takes seriously. This is of course not a random sample of studies, as the meta-analysis filtered based on its criteria.

Quick interjection, to those living under a rock: Covid-19 is the disease caused by SARS-CoV-2, the virus causing the pandemic of 2020. The IFR should be thought of as the probablity of someone dying, given that they are infected (by SARS-CoV-2). Of course, this varies based on various factors (like age and quality of medical care received), so there is not a single IFR. If one is calculating only a single IFR, then statistically, one is already in a state of sin. But our models are not reality – they have to simplify somewhere. Some people define the IFR as the exact proportion of dead people amongst the infected in some sample. Those people are wrong, in the sense that the IFR defined this way is not meaningful for trying to reason about the future.

We can only estimate the number of infected people, not know it exactly. A popular method is to run antibody tests to infer how many people were infected. I limited myself to studies that did antibody tests as I have little confidence in the alternatives (such as running unvalidated epidemiological models).

I only looked at studies from the US/Europe. I have no affiliations with any of the authors. I did not evaluate study design, just the statistics. Dicey questions nobody knows answers to, like question related to the “true” specificity of various antibody tests (the specificity you calculate when you compare to PCR has some selection effects “built in” because your PCR positives might be people who are on average sicker), were ignored. The point was to see if there were many obvious statistical mistakes – my area of expertise as a mathematician is not statistics, so I catch only the obvious ones. I let things that looked vaguely fishy (like various “corrections” for things by rescaling them) slide. Of course, all of the statistical methods should have been decided before looking at the data, I don’t think any study mentioned doing this – I let this (huge) point slide for all.

Why not publish this as a meta-analysis as part of the scientific process™ in a journal?

It’s borderline rude to openly criticize work of others as an outsider in the fields I typically publish research in. I’m an outsider (I have never met an epidemiologist), so I didn’t expect much success here.

Now without futher ado:

The Great

• The paper by Stringhini et al., and this one from the same group are both excellent. I hope they win some kind of award.

The Good-to-Not-so-Good, it’s hard to objectively label these, maybe it’s just not reasonable to expect more than one study on the level of Stringhini et al.

A typical mistake was that authors did not realize that assay validation does not give exact sensitivities/specificities, but just an uncertainty-ridden estimate. I abbreviate this mistake with DNCTU (“does not consider test uncertainty”), see part III of the post linked here for further information.

Some studies mention an IFR, but do not give a confidence interval. Typcially, the aim of those studies is not to estimate the IFR. I will abbreviate this with NICI (“no IFR confidence intervals”).

• A study from the English Office of National Statistics that uses the word “Bayesian model” and includes the sentence “Because of the relatively small number of tests and a low number of positives in our sample, credible intervals are wide and therefore results should be interpreted with caution”. Note that this study does not do much, but also does not claim to do much, saying that they do not know sensitivity and specificity of the test. Nice. A newer version contains various scenarios for sensitivity/specificity and their implications, without committing to a specific scenario. Somewhat weirdly, the meta-analysis mentioned above still includes a single confidence-interval for the IFR “from” this study.
• Rosenberg et al. have a study that seems ok. The statistics are a bit simplistic, also DNCTU (well, they do do a “sensitivity analysis”, but the abstract contains confidence intervals that don’t include this) and NICI.
• This study from Herzog et al. They note that “Moreover, the sensitivity of the serological test used in this study depends on the time since the onset of symptoms” and have other sentences like this which to me suggests they were being thorough. Then again, their samples come from “ambulatory patients visiting their doctors” (excluding hospitals+triage centers) – I’m not sure you can treat this as a random sample of the population, which (to their credit) they do talk about briefly. They don’t do their own tests for sensitivity/specificity, but refer to a study for their equiptment giving a “sensitivity ranging from 64.5% to 87.8%”, which is a huge range. Though they do a “sensitivity analysis” to this in the supplementary material, it looks like they use only the larger value in the results section, so DNCTU.
• The Bendavid et al study received much attention due to its mistakes early on, including from well-known figures like Andrew Gelman. The authors then tried to fix their result, but there were further cricisisms saying their confidence intervals are (substantially) too small.

The <insert-polite-euphemism-for-Bad> but my standards are high..

• To some extent, this blog post – I didn’t pre-commit to objective criteria when deciding which category to put things in. I also didn’t check the authors’ work – when they said some 95% confidence interval is something, I believed them. I’d also like to use this space to say that having a study in this section shouldn’t be seen as an attack on the authors (who are probably all wonderful people), just the part of their work which is the statistical analysis. The part that isn’t statistical analysis can still be (very) valuable data! Please remember the Andrew Gelman quote referenced above: “we have to accept statistical incompetence not as an aberration but as the norm”. As far as I’m concerned, even the studies in this section are probably excellent when compared to the field of epidemiology in general.
• This study from Menachemi et al. includes the sentence “Whereas the laboratory-based negative percent agreement was 100% for all tests, the positive percent agreement was 90% for one RT-PCR test and 100% for the others” without saying how many samples this validation based on. Their antibody test boasts a stellar 100% sensitivity, along with a 99.6% specificity, which seems unrealistically high, but I’m not an expert. It isn’t clear to me whether they even try to account for false positives/negatives (obviously, also DNCTU), and NICI. No raw data to be directly analyzed.
• Snoeck et al. did a study which is missing confidence intervals in their “Results” section (they might be elsewhere). Sentences like “Our data suggests that between April 16 and May 5 there were 1449 adults in Luxemburg that were oligo- or asymptomatic carriers of SARS-Cov-2”, with no confidence intervals whatsoever (the confidence interval they calculate elsewhere for this figure is [145, 2754] – I hope the first number is a typo). Prevalence is really low (35 of 1862 have positive antibody test), so you’d expect uncertainty to play a huge role. However, they don’t explicitly even say that they correct for false positives/negatives, I guess not (“The formula for infection rate was as follows: past or current positive PCR or IgG positive or intermediate divided by the total sample population (N=1835).”). Then again, they mention test validation so I’m very confused. Ad hoc exclusions of 12 people people aged >79 because they didn’t have enough people in this group for it to be “representative”, same with 3 people they couldn’t classify as male/female. At least they have lots of raw data that can be analyzed.
• Streeck et al. decide that they want to estimate the IFR, but decide also that IFR in this context with 7 deaths should mean “number of people who died in our sample divided by how many were infected”. This is like deciding that the probability of getting heads in a fair coin is definitely 3/4 based on 4 coin flips where you got tails once. I grudgingly admit that they mention that this is how they define IFR, together with some arguments on how everyone does it this way when studying covid-19.

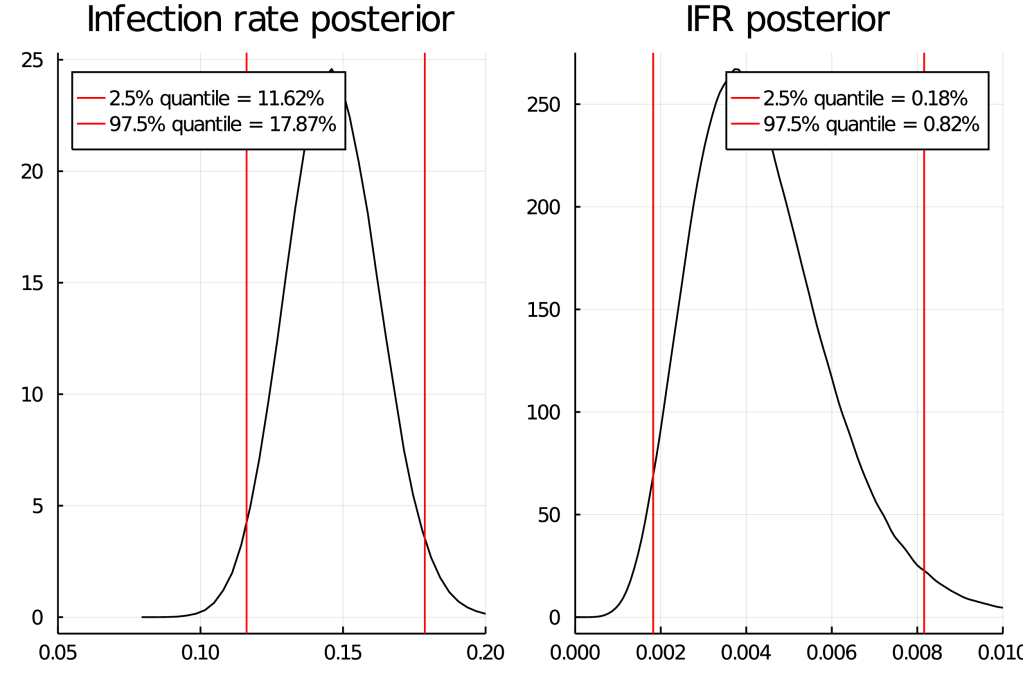
This study does essentially 3 different tests (PCR, antibody, asking people whether they had positive PCR test in the past) and when some people who previously had a positive PCR test don’t antibody-test positive, they don’t treat these as antibody false-negatives but (as far as I can tell) add them to the (already corrected for false-negatives) positives based on antibodies. I mean sure, it’s only 2 of 127 positive results, but still… Far worse than this, they then decide that because their sample has 2.39% of people previously testing PCR positive, but the general population is 3.08%, it is legitimate to “correct” by a factor of 1.29 – this is deep in garden of forking paths territory, luckily values obtained by this “correction” do not make it into the abstract. To their credit, (some) of their raw data is available in various tables. DNCTU with the questionable claim that “independent analysis of control samples” in which 2 of 109 = 98.3% were positive confirm the high (99.1% using 1656 samples) specificity claims of the manufacturer. That’s almost twice the (naively calculated) false positive rate! I mean sure, maybe they were just unlucky, but still…

• The meta-analysis itself. As you can see, most of these studies did not calculate the IFR. So what is done? “For the studies where no confidence interval was provided, one was calculated”. Of course, uncertainty in this “calculation” doesn’t seem to be included, see the point about Streeck et al. Further uncertainties that the individual papers provide (such as talking about multiple scenarios that would give different ranges) seem to be swept under the rug. The results are then “aggregated” into a single confidence-interval, with authors saying “there remains considerable uncertainty about whether this is a reasonable figure or simply a best guess” which is a weird thing to say about a confidence interval. Maybe make the confidence interval bigger if you aren’t so confident? There is of course also the issue of including lots of data that doesn’t correct for test sensitivity/specificity, which is just unacceptable. A meta-analysis is only as good as the studies it includes, and if many of these are bad you don’t benefit from including a few good ones.

The is-this-even-science?

A number of studies used in the meta-analysis weren’t studies as much as various governments saying “let’s give antibody tests to lots of people and then say how many were positive”. There is no accounting for false positives/negatives, and no real statistical analysis whatsoever. The meta-analysis nevertheless uses these, which is why I have a section for them

• A study from the Spanish government, that appears to be preliminary data for this study in The Lancet by Pollàn et al. That study itself is not bad (though: no propagation of test uncertainties, has some statistical corrections that should have been pre-registered, 100% specificity for IgG antibody test based on 53 tests of serum and 103 tests of blood [note of course, that this relative to PCR-positive cases, which may bias towards symptomatic cases, which they of course do not mention] is assumed), but given that the meta-analysis doesn’t cite it, I’m not going to assume the meta-analysis uses the study and I can’t find the “preliminary data” they reference.
• This study from Slovenia, which fits the description above exactly.
• Some preliminary findings of a Czech ‘study’, the only results I can find are news articles like this one.
• A Danish study, again seems to fit the exact description.
• Some survey results from Finland, as above.
• The NYC serology studies, as above, a paper here is what the meta-analysis cites.

Conclusion

Hard to say. I went into this expecting lots of really bad studies (it didn’t help that Streeck et al. was the first one read after the meta-analysis), and reading studies seemed to confirm this. Now that I re-read all of my reviews above I feel like it’s not all bad – the worst statistical offense of most studies is not propagating uncertainties in their test validation, which is bad but not necessarily fatal. My main preconception – that scientists are often far more confident about their results than they have a right to be – was not shaken.

Somewhat soberingly, the study that tends to be most important – the meta analysis – appears to be easiest to make large mistakes in. This is ironic, as the aim of a meta-analysis is to try to fix issues that individual studies might have. I don’t understand why nobody does a statistically correct meta-analysis (while accounting for age) with something like stan. So I guess I’ll have to be the one to do it – the first step will be to decide and to pre-register the statistical methods used. Please contact me at mwacksen_at_protonmail.com if you are interested in collaborating, I would love to not have to work on this alone.

I recently became aware of the meta analysis by Ioannidis, but I’m not convinced by its statistics either – I just can’t see any rigorous uncertainty quantification apart from “here’s the median of the IFR we “infer” from studies” . I guess implicit in this kind of thing is that you expect “scientist mistakes” to bias results equally in both directions, so the “truth” is somewhere in the middle.

Some remaining comments on the IFR

I am unqualified to assess four important questions:

• How many covid-19 infected people get antibodies after?
• How many of the deaths in official deaths counts were deaths “of” covid-19 as opposed to deaths “with” covid-19?
• How many deaths of covid-19 were missed?
• How random were the antibody samples really?

These questions were of course raised by a number of the studies mentioned. The question of the “real” IFR of course crucially depends on these. I am therefore unqualified to assess the “validity” of various IFR estimates.